This isn’t a binary tree. No, this is a spaghetti tree, using a Dictionary as its branches. (No, this is not a real data structure. Don’t tell your professor, you’re optimizing spaghetti trees)
Is this faster than taking all the keys, and producing a unique key? It’s not definitive, but the Dictionary Tree starts out of the gate definitively faster. But then after a depth of 10, it becomes uncertain. Eventually searching for keys, faster. Is this b/c using so many instances of a Dictionary, forces reads from something other than the cache? The world may never know.
public class SingleLookupNode{public TPayload Payload { get; set; }public readonly Dictionary<TKey, SingleLookupNode<TKey, TPayload>> Branches = new Dictionary<TKey, SingleLookupNode<TKey, TPayload>>();}
Now you’re probably wondering if I’ve finally fell off my rocker by taking too much of whatever gets my head so red.
Confession
Actually as an undergraduate, I admired the binary tree’s ability to grow with the data, vs hashtable’s space efficiency and collisions needing constant managing. It’s why I still hold onto using recursive tree/graph structures so much. But I think it obvious by now, it’s way faster to “compute a formula” with 100 characters, than compare log(100) characters.
Well, yes, that is always a problem. But back to the problem space, why hasn’t any one else needed to access data in a hierarchical format. And there are dozens of ways to do this in C#, but none built into the framework. And seriously, do you really want to implement a binary tree, with only left and right branches? You could be comparing “forever”. Which leaves an obvious question, if you needed the Address for “USA”–>”NY”–>”Kings Cty”–>”John Doe”, is it faster to search for “USA|NY|Kings Cty|John Doe” (a kind of a hash, since that is what the dictionary is doing in the background) in the one Dictionary, or to search for it in a nested tree structure like above?
Food for Thought
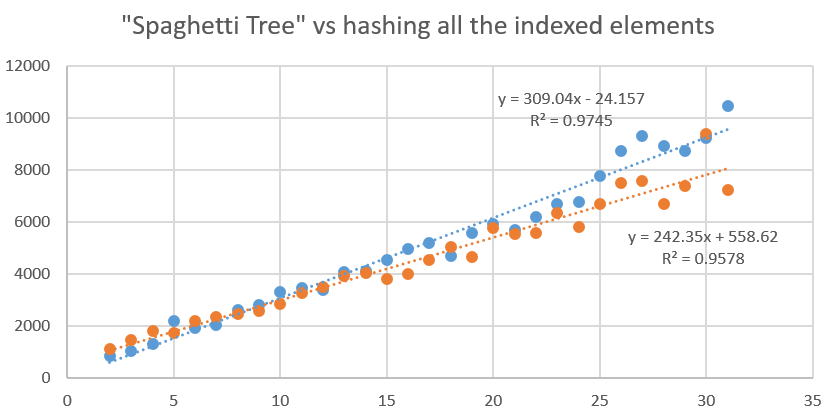
Notice how the graph’s performance has a regular wave to it? I suspect that’s garbage collection in the background. But it didn’t rear it’s ugly head during array testing.
The graph may show a runaway win for hashing every key produces definitively faster results. But notice at depths less than 8, the tree structure seems to always come out on top. But after that, it seems there is less cost constructing the “hash”, than traversing and comparing several trees.
depth dictree rehashtree baseline delta 2 828 (672) 1094 (938) 156 -266 3 1016 (828) 1437 (1249) 188 -421 4 1281 (1094) 1813 (1626) 187 -532 5 2172 (1937) 1734 (1499) 235 438 6 1922 (1704) 2172 (1954) 218 -250 7 2032 (1814) 2328 (2110) 218 -296 8 2610 (2375) 2437 (2202) 235 173 9 2797 (2547) 2578 (2328) 250 219 10 3282 (3001) 2828 (2547) 281 454 11 3437 (3156) 3266 (2985) 281 171 12 3360 (3063) 3500 (3203) 297 -140 13 4078 (3734) 3922 (3578) 344 156 14 4109 (3796) 4047 (3734) 313 62 15 4515 (4218) 3782 (3485) 297 733 16 4938 (4563) 3984 (3609) 375 954 17 5187 (4562) 4547 (3922) 625 640 18 4687 (4327) 5032 (4672) 360 -345 19 5578 (5187) 4656 (4265) 391 922 20 5922 (5532) 5766 (5376) 390 156 21 5672 (5297) 5547 (5172) 375 125 22 6187 (5796) 5578 (5187) 391 609 23 6703 (6297) 6359 (5953) 406 344 24 6782 (6376) 5812 (5406) 406 970 25 7750 (7329) 6688 (6267) 421 1062 26 8750 (8156) 7516 (6922) 594 1234 27 9328 (8750) 7594 (7016) 578 1734 28 8907 (8423) 6703 (6219) 484 2204 29 8734 (8281) 7391 (6938) 453 1343 30 9219 (8609) 9391 (8781) 610 -172 31 10468 (10030) 7219 (6781) 438 3249
No code provided. I think the test description should be satisfactory. Though, not for me. I actually use the “spaghetti tree”, in a HTMLParser and other “language interpreter”-like functions. More on that later.